-
-
پيوندها
- فروش ساعت مچی" title="" target="_blank" >فروش ساعت مچی
- مرجع فناوری و تکنولوژی(نارنجی)
- سایت تخصصی علوم تجربی
- اپراتور رایتل
- وبسایت شخصی مهندس ساکت
- فیزیک
- ساعت رومیزی ایینه ای
- رقص نور لیزری موزیک
- قالب رز بلاگ
-
آرشيو
-
پيوندهاي روزانه
-
آخرين نوشته هاي من
- ناپلئون بناپارت
- لویی شانزدهم
- عکس هایی از ایسلند
- با پاریس اشنا شوید
- اندام تناسلی زن
- سیستم ادراری
- لویی پاستور
- مکانیک کوانتوم
- برو به ادامه مطلب
- نظریه اشوب
- اینتل از ویلچر هوشمد خود برای استیون هاوکینگ پرده برداشت
- اطلاعاتی در مورد ابراهام لینکلن
- لوئی دوازدهم
- بیایید ایزاک اسیموف را کمی بهتر بشناسیم.
- فرانسیس بیکن که بود؟
- مطالبی در مورد بیوشیمی
- زیست سلولی و مولکولی چیست؟؟؟؟؟؟؟؟؟
- بافت ابکش
- آلانین آمینوترانسفراز
پربازديدترين ها
- الت تناسلی مرد چیست؟
- پرچم در گل چیست؟
- ماشین های تورینگ
- مکتب فیثاغورثیان
- امیلاز چیست؟
- نقد و بررسی نوکیا دویست و شش
- کتب ریاضی
- عصر رنسانس
- هورمون انژیوتانسین چیست؟
- هندسه تحلیلی چیست؟
- جابر ابن حیان
- حسابان
- هندسه2
- قرون وسطی
- اسپرم
- منظومه شمسی
- فئودالیسم
- زبان المانی
- رنسانس 2
- تار (ساز)
- زمین شناسی چیست؟
- اقتصاد
- علم ترکیبیات
- فیودور داستایوسکی که بود؟
- برنامه نویسی
- طلا
- خون
- ژایگاه داده چیست؟
- هورون اکسی توسین چیست؟
- عدد جبری
- منطق فازی
- نقد و بررسی نکسوس 10
- نقد و بررسی نوکیا لومیا نهصد و بیست و پنچ(طرح نقد و بررسی موبایل)
- مطلبی در مورد انقلاب کبیر فرانسه
- ترکیبات کووالانسی
- معرفی چند کتاب ریاضی
- نقد وبررسی نوکیا اشا سیصد و پنج(طرح معرفی موبایل)
- نجوم رصدی
- دستگاه عصبی
- برای نجومی ها
- پیوند هیدروژنی
- شرکت ال جی
- زیست سلولی و مولکولی چیست؟؟؟؟؟؟؟؟؟
- نقد وبررسی نوکیا لومیا نهصد وبیست(طرح معرفی موبایل)
- جنگ جهانی دوم
- دانشمند ریاضی
- ترکیب گزاره های ریاضی 1
- پارادوکس
- ژاپن
- معرفی بعضی از دانشمندان شیمی
مطالب تصادفی
-
موضوعات وبلاگ
- تایپک کامپیوتر
- مبانی کامپیوتر تعداد پست ها: 7
- برنامه نویسی تعداد پست ها: 1
- تبلت.اولترابوک.نوت بوک تعداد پست ها: 19
- تاریخچه کامپیوتر ها تعداد پست ها: 5
- تایپک علوم تجربی
- فیزیک تعداد پست ها: 17
- شیمی تعداد پست ها: 15
- زیست شناسی تعداد پست ها: 33
- زمین شناسی تعداد پست ها: 3
- تایپک اختر شناسی و نجوم
- تایپک ریاضی
- هندسه تعداد پست ها: 10
- جبر و انالیز تعداد پست ها: 11
- منطق تعداد پست ها: 13
- کتب ریاضی تعداد پست ها: 5
- علوم اجتمایی
- تاریخ تعداد پست ها: 21
- جغرافیا تعداد پست ها: 6
- اقتصاد تعداد پست ها: 4
- فلسفه و الهیات
- موسیقی
- کلاسیک تعداد پست ها: 0
- سنتی تعداد پست ها: 2
- معرفی ساز ها تعداد پست ها: 3
-
-
-
امکانات وبلاگ
نام : وب : پیام : 2+2=: (Refresh)  خبرنامه وب سایت:
خبرنامه وب سایت:
 آمار
وب سایت:
آمار
وب سایت:
بازدید امروز : 52
بازدید دیروز : 0
بازدید هفته : 58
بازدید ماه : 227
بازدید کل : 90371
تعداد مطالب : 178
تعداد نظرات : 11
تعداد آنلاین : 1 -
طراح قالب: NEGASH.IR
ارائه کننده متفاوت ترين قالب ها براي سرويس هاي وبلاگدهي فارسي
-
درباره من
با سلام. من محمد حسن ابوالحسنی هستم.من دانش اموز سمپاد هستم و به وبلاگنویسی علاقه دارم.موضوعات کلی این وبلاگ شامل علوم پایه و نجوم و علوم اجتماعی و .. است.امید وارم از این وبلاگ خوشتان بیاید.
پروفايل من -
آخرین ارسال های انجمن
عنوان پاسخ بازدید توسط ForumPostCountAnswer [ForumPostLastAuthor] [] [loxblog] نويسنده: [cb:post_author_name] | [cb:post_create_date] ساعت [cb:post_create_time]
پیوند هیدروژنیعلوم طبیعت > شیمی > شیمی معدنی
هرگاه هیدروژن به اتمی با الکترونگاتیوی زیاد مثل فلوئور ، اکسیژن یا نیتروژن متصل گردد، شرایطی برای بوجود آمدن نوع بسیاری مهمی جاذبه بین مولکولی مثبت ـ منفی که آن را پیوند هیدروژنی میگویند حاصل میشود. به عبارت دیگر ، اتم هیدروژن یک مولکول و زوج الکترون غیر مشترک مولکول دیگر متقابلا همدیگر را جذب میکنند و پیوندی تشکیل میشود که به پیوند هیدروژنی ، Hydrogen Bond مرسوم است.
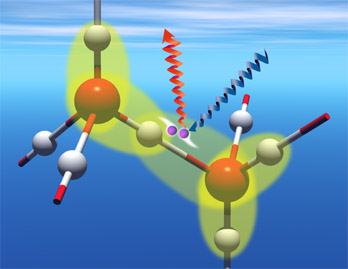
اطلاعات اولیه
دربرخی از
بطور غیرعادی قوی است. این جاذبه در ترکیباتی مشاهده میشود که درآنها بین هیدروژن و
که اندازه کوچک و
زیاد دارند، پیوند هیدروژنی وجود دارد. پیوند هیدروژنی نه تنها بین مولکولهای یک نوع ماده ، بلکه بین مولکولهای دو ماده متفاوت که توانایی تشکیل پیوند هیدروژنی را دارند نیز برقرار میشود.
نحوه تشکیل پیوند هیدروژنی
پیوند هیدروژنی بر اثر جاذبه اتم هیدروژن اندک مثبت موجود در یک مولکول و اتم بسیار الکترونگاتیو
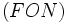
موجود در مولکول دیگر (یا در محل دیگر همان مولکول اگر مولکول به قدر کافی بزرگ باشد که بتواند روی خود خم شود) تولید میگردد. جا به جا شدن یک
به سمت عنصر بسیار الکترونگاتیو نیتروژن ، اکسیژن یا فلوئور موجب میشود که این اتمها دارای بار منفی جزئی شوند.
در این صورت پیوند هیدروژنی پلی است میان دو
شدیدا الکترونگاتیو با یک اتم هیدروژن که از طرفی بطور
با یکی از اتمهای الکترونگاتیو و از طرف دیگر بطور
(جاذبه مثبت به منفی) با اتم الکترونگاتیو دیگر پیوند یافته است. استحکام پیوند هیدروژنی
یکدهم
تا
یکپنجاهم
قدرت یک
متوسط است.
شرایط تشکیل پیوند هیدروژنی
- بالا بودن الکترونگاتیوی اتمهای متصل به هیدروژن: برهمین اساس است که فلوئور (الکترونگاتیوترین عنصر) ، قویترین پیوند هیدروژنی و اکسیژن (الکترونگاتیوتر از نیتروژن) ، پیوند هیدروژنی قویتری درمقایسه با نیتروژن تشکیل میدهد. همچنین بار مثبت زیاد بر روی اتم هیدروژن ، زوج الکترون مولکول دیگر را بشدت جذب میکند و کوچک بودن اندازه اتم هیدروژن سبب میشود که ملکول دوم بتواند به آن نزدیک شود.
- کوچک بودن اتمهای متصل به هیدروژن : پیوند هیدروژنی واقعا مؤثر فقط در ترکیبات فلوئور ، اکسیژن و نیتروژن تشکیل میشود. با وجود اینکه دو اتم نیتروژن و کلر ، الکترونگاتیوی برابر دارند، چون اتم کلر از اتم نیتروژن بزرگتر است بر خلاف نیتروژن ، کلر پیوند هیدروژنی ضعیفی تشکیل میدهد.
توجیه خواص غیرعادی برخی از مواد
وجود خواص غیرعادی برخی از مواد در حالت
یا
از جمله بالا بودن دماهای ذوب و جوش ، نشان میدهد که نیروهای جاذبه بین مولکولی در آنها به اندازهای زیاد است که نمیتوان آن را به تأثیرهای متقابل ضعیف بین مولکولی نسبت داد. آشناترین این نوع مواد ، فلوئورید هیدروژن ، آب و آمونیاک است که بسیاری از خواص آنها از جمله دماهای جوش و ذوب آنها از دماهای جوش و ذوب ترکیبهای مشابه خود ، برای مثال
بطور غیرمنتظرهای بالاتر است.
شاید تصور شود که علت این وضعیت غیر عادی ، قطبیت به نسبت زیاد این مولکولهاست. البته تا اندازهای همین طور است. اما بررسی دقیق این پدیده غیر عادی نشان میدهد که باید نیروی جاذبه قویتر از نیروهای جاذبه دوقطبی _ دوقطبی بین مولکولهای آنها برقرار باشد.
اگر به ساختار الکترونی مولکولهای
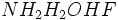
توجه شود، میتوان به موردهای مشترک بین آنها پی برد. این وجه اشتراک ، وجود دست کم یک پیوند کوالانسی با اتم هیدروژن و یک
دو الکترونی اتم مرکزی بسیار الکترونگاتیو در هر یک از آنهاست.
اتمهای
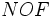
الکترونگاتیوی بالایی دارند با هیدروژن پیوند کوالانسی بشدت قطبی بوجود میآورند، بطوری که هیدروژن به میزان قابل توجهی خصلت یک
را پیدا میکند. جفت الکترون ناپیوندی و قابل واگذاری روی اتم الکترونگاتیو H ، این امکان را پدید میآورد که اتم هیدروژن در نقش پل ، اتمهای الکترونگاتیو دو
را به یکدیگر متصل کند و نیروی جاذبه بین مولکولی بوجود میآید که به پیوند هیدروژنی مرسوم است.
خواص ترکیبات دارای پیوند کووالانسی
ترکیباتی که مولکولهای آنها از طریق پیوند هیدروژنی به همدیگر پیوستهاند، علاوه بر دارا بودن
بالا ، بطور غیرعادی در دمای بالا
میشوند و
،
و
آنها زیاد است.
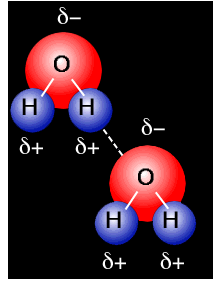
علت شناور بودن یخ
روی آب شناور میماند، زیرا به هنگام
، منبسط میشود. سبب این انبساط پیوند هیدروژنی میان مولکولهای خمیده آب است ساختار خمیده یا زاویهای مولکول آب ناشی از آرایش چهار وجهی چهار جفت الکترون در
یک اتم است. ساختار زاویهای
و پیوند هیدروژنی میان مولکولهای آب به آن معنی است که هر مولکول آب میتواند حداکثر با چهار مولکول آب دیگر پیوند هیدروژنی داشته باشد.
پس آب مایع را میتوان به صورت خوشههایی از مولکولهای آب تصورکرد، خوشههایی که با پیوند هیدروژنی از مولکولهای آب ساخته شدهاند و دائم در حال حرکتند. شمار مولکولها در هر خوشه و سرعت حرکت خوشهها به
بستگی دارد. با سرد شدن آب ، مجموعههایی از مولکولهای آب که بسرعت در حرکتاند، کند میشوند و در نقطه انجماد به یکدیگر قلاب شده ساختمان سه بعدی منبسط شدهای را بوجود میآورند. این ساختمان گستردهتر موجب میشود که تراکم یخ کمتر از آب باشد.
ذوب شدن یخ در حدود 15% انرژی پیوندهای هیدروژنی را میشکند و این امر سبب فرو ریختن ساختار میشود. در نتیجه مایعی متراکم حاصل می گردد.
چرا نقطه جوش آب بالا است؟
خاصیت عجیب دیگر آب ، نقطه جوش نسبتا زیاد آن است. تقریبا تمام ترکیبات هیدروژندار مجاور اکسیژن و اعضای خانواده آن یعنی
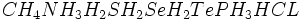
در دمای اتاق به حالت گازی هستند. اما آب مایع است. برای آنکه یک مولکول به حالت
در آید، باید انرژی جذب کند تا بتواند خود را از قید مولکولهای دیگر آزاد کند. چون آب مایع با پیوند هیدروژنی به صورت خوشههایی از مولکولها در میآید، برای شکسته شدن پیوندهای هیدروژنی آن ، انرژی زیادی لازم است.
اما همه پیوندهای هیدروژنی شکسته نمیشوند و خوشههایی از مولکولهای آب حتی در نزدیکی 1000 درجه سانتیگراد هنوز وجود دارند. وقتی آب گرم میشود، آشفتگی گرمایی پیوند هیدروژنی را میگسلد تا آنکه در
، فقط جزء کوچکی از شمار پیوندهای هیدروژنی موجود در آب مایع یا جامد باقی میماند. اگر پیوند محکم میان مولکولی از قبیل پیوند هیدروژنی وجود نداشته باشد، مواد معمولا بنا به
خود به جوش میآیند.
جرمهای مولکولی بزرگتر برای جوش آمدن به دمای زیادتری نیازمندند. عمدتا به این دلیل که
بزرگتر آسانتر و پیچیده میشوند و این امر ، منجر به
بین مولکولی قویتر میشود.
کاربردهای پیوند هیدروژنی
پیوندهای هیدروژنی در بسیاری از مواد یافت میشوند. پدیدههایی از قبیل چسبناک شدن آبنبات سفت ، دیرتر خشک شدن الیاف
از الیاف
، نرم شدن
با نایلون ، ناهنجارهای ظاهری در ماهیت آب ، همگی ناشی از همین پیوندهای هیدروژنی است.
موضوع : تایپک علوم تجربی , فیزیک , شیمی , زیست شناسی , ,
امتیاز : نتیجه : امتیاز توسط نفر مجموع امتیاز :
برچسب ها : پیوند هیدروژنی , پیوند کوالانسی , هیدروژن ,
بازدید : 2173 نويسنده: [cb:post_author_name] | [cb:post_create_date] ساعت [cb:post_create_time]
عبه اطلاعات فیلسوف |عنوان= فارابی |سرشناسی= |تصویر =
 |نام کامل= ابو نصر محمد بن محمد فارابی |لقب= معلم ثانی |نسب= |حیطه= |دوره= |مکتب= |تاریخ تولد= سال ۲۶۰ هجری |شهر تولد= فاراب، خراسان. |کشور تولد=ایران |تاریخ مرگ= |شهر مرگ= دمشق |کشور مرگ= سوریه |ملیت = ایرانی العصل (در قرن های گذشته کشور های زیادی دنبال بدست اوردن دانشمندان ایرانی بودند و هستند و سعی در تحریف تاریخ دارند ) |مدفن= |نام همسر= |فرزندان= |دین= |مذهب= |تأثیرگرفته از=ارسطو٬ افلاطون٬ فلوطین |تأثیرگذار بر= ابن سینا، سهروردی٬ ملاصدرا |استادان= یوحنا بن حیلان |شاگردان= یحیی بن عدی |تالیفات= ،
|نام کامل= ابو نصر محمد بن محمد فارابی |لقب= معلم ثانی |نسب= |حیطه= |دوره= |مکتب= |تاریخ تولد= سال ۲۶۰ هجری |شهر تولد= فاراب، خراسان. |کشور تولد=ایران |تاریخ مرگ= |شهر مرگ= دمشق |کشور مرگ= سوریه |ملیت = ایرانی العصل (در قرن های گذشته کشور های زیادی دنبال بدست اوردن دانشمندان ایرانی بودند و هستند و سعی در تحریف تاریخ دارند ) |مدفن= |نام همسر= |فرزندان= |دین= |مذهب= |تأثیرگرفته از=ارسطو٬ افلاطون٬ فلوطین |تأثیرگذار بر= ابن سینا، سهروردی٬ ملاصدرا |استادان= یوحنا بن حیلان |شاگردان= یحیی بن عدی |تالیفات= ،
ابو نصر محمد بن محمد فارابی معروف به فارابی، (حدود سال ۲۶۰ هجری، در فاراب، خراسان، ترکمنستان امروزی – سال ۳۳۹ هجری در سن ۸۰ سالگی[۱])از بزرگترین فیلسوفان ایرانی [۲] شرقی سده سوم و چهارم هجری است. اهمیت او بیشتر به علت شرحهایی است که بر آثار ارسطو نگاشته و به سبب همین مشروحات او را معلم ثانی خواندهاند و در مقام بعد از ارسطو قرار دادهاند. وی آثاری نظیر «»، «»، «» و «والدین فارابی ایرانی تبار بودند.خود او نیز ایرانی العصل بوده و کشورهایی همچون ترکمنستان و ... دنبال تحریف تاریخ به نفع خود بوده و می خواهند او را از کشور خود معرفی کنند . [۳][۴] و نوشتهاند که ابونصر از نژاد ایرانی بودهاست (= واصله فارسی / کان من سلاله فارسیه).[۵]
محتویات
زندگی
ابونصر محمد بن محمد طرخانی ملقب به فارابی، در حدود سال ۲۵۷هجری قمری/ ۸۷۰میلادی در دهکدهٔ «فاراب) در فرارود (شهر اُترار کنونی در جنوب قزاقستان) یا پاریاب (فاریاب) خراسان در افغانستان کنونی به دنیا آمد.دهخدا به نفل از بدیع الزمان فروزانفر مینویسد:«اسم پدراو طرخان و نام جدش اوزلوغ است. درشرح زندگی فارابی مطلبی که بر جریان واقعی زندگی دوران طفولیت و جوانی وی باشد در کتابها وجود ندارد. ابن ابی اصیبعه دو خبر متناقض درباره او نقل میکند: اول اینکه فارابی در آغاز کار نگهبان باغی در دمشق بودو دوم اینکه، در عنفوان جوانی به قضاوت مشغول بود و چون به معارف دیگر آشنا شد، قضاوت را ترک کرد و با تمام میل به طرف معارف دیگر روی آورد. »در جوانی برای تحصیل به بغداد رفت و نزد «متی بن یونس» به فراگرفتن منطق و فلسفه پرداخت. سپس به
در سال ۳۳۰هجری قمری/۹۴۱میلادی به دمشق رفت و به «سیف الدوله حمدانی» حاکم حلب پیوست و در زمره علمای دربار او درآمد. فارابی در سال ۳۳۸هجری قمری/۹۵۰میلادی در سن هشتاد سالگی در دمشق وفات یافت. عده ایی بر این باورند که ابونصر هنگامی که از دمشق به عسقلان میرفت به دزدان برخورد. ابونصر گفت:« هر آنچه از مرکب، سلاح، لباس ومال هست بگیرید و با من کاری نداشته باشید.» آنها نپذیرفتند و قصد کشتن او کردند. ابونصر به ناچاربا آنها جنگید و کشته شد.امرای شام از حادثه با خبر شدند. ابونصر را دفن کردند و دزدان را بر سر قبر او دار زدند.
مورخان اسلامی معتقدند که فارابی فردی زهد پیشه و عزلتگزین و اهل تامل بود. اعراض او از امور دنیوی به حدی بود که با آن که برایش از بیتالمال حقوق بسیار تعیین کرده بود، به چهار درهم در روز قناعت میورزید.
فارابی در انواع علوم بی همتا بود. چنانکه دربارهٔ هر علمی از علوم زمان خویش کتاب نوشت و از کتابهای وی معلوم میشود که در علوم زبان و ریاضیات و کیمیا و و موسیقی و الهیات و علوم مدنی و فقه و منطق دارای مهارت بسیار بودهاست.
درست است که کندی نخستین فیلسوف اسلامی است که راه را برای دیگران پس از خود گشود؛ اما او نتوانست مکتب فلسفی تأسیس کرده و میان مسائلی که مورد بحث قرار دادهاست، وحدتی ایجاد کند. در صورتی که فارابی توانست مکتبی کامل را بنیان نهد.
ابن سینا او را استاد خود میشمرد و ابن رشد و دیگر حکمای اسلام و عرب، برایش احترام بالایی قائل بودند. ازجمله سخنی از ابن سینا است که اوج منزلت علمی اورا بیان می کند:کتاب مابعدالطبیعه را مطالعه کردم وبعد از چهل مرتبه مطالعه نتوانستم ازاغراض مولف آن اگاهی پیداکنم تا اینکه در بازار به کتابی از ابونصر فارابی برخورد کردم که شرحی بر کتاب مابعد الطبیعه بود بعد ازمطالعه آن توانستم مطالب مابعد الطبیعه را در یابم وبسیار مسرور شدم.
در سنت فلسفه اسلامی، فارابی را بعد از ارسطو که ملقب به «معلم اول» بود، معلم ثانی لقب دادهاند.
نسب فارابی
تاریخ نگار عرب ابن ابی عصیبه (وفات ۶۶۸ ه.ق) در کتاب اویون خود اشاره کردهاست که فارابی که پدر قرآن است از نسب پارسی بود.[۶][۲] ابن ندیم در الفهرست خود، و نیز [۷][۸] علاوه بر اینها فارابی در حاشیه بسیاری از کارهایش به زبان پارسی و سغدی منابعی را معرفی کرده (حتی به زبان یونانی، اما به ترکی نه)[۲]),[۹] حتی زبان سغدی به عنوان زبان مادری وی [۱۰] و زبان ساکنان فاراب دانسته شدهاست.[۱۱] محمد جواد مشکور ایرانی زبان بودن اصالت آسیای میانه را استدلال کردهاست.[۱۲] اما فاراب در درجه نخست جزو سرزمین مسلمانان بود و در درجه نخست فارابی به دنیای اسلام و تمام بشریت تعلق دارد و عرب یا پارسی یا ترک بودن وی اهمیتی ندارد.[۱۲] اصالت پارسی فارابی توسط دیگر منابع نیز بحث شدهاست.[۱۳] همچنین پروفسور دانشگاه آکسفورد آقای بوسورث مینویسد که چهرههای بزرگ مانند فارابی، بیرونی و ابن سینا توسط دانش پژوهان علاقمند ترک به نژاد ترکی چسبانده شدند.[۱۴] در دانشنامه ایرانیکا دکتر گوآتاس اظهارات ابن خلکان را نکوهش کرده و مدارک پیش از وی در این زمینه از ابن عصیبه در مورد پارسی بودن فارابی باعث شده تا ابن خلکان به تلاش برای مدرکسازی جهت ترک نشان دادن وی باشد.[۲] در این چهارچوب وی اشاره میکند که ابن خلکان ابتدای اسم فارابی نسبت الترک را افزود در حالی که فارابی هرگز چنین نسبتی را نداشتهاست.[۲]
 اسکناسی که هم اکنون در جمهوری قزاقستان رواج دارد
اسکناسی که هم اکنون در جمهوری قزاقستان رواج داردقدیمیترین کسی که نسب فارابی را ترک دانسته ابن خلکان بودهاست. وی در اثر خود وفایات فارابی را متولد فاراب و روستای کوچکی به اترار در قزاقستان شناخته میشود و از والدینی ترک میداند. برخی منابع دیگر نیز به این جریان معتقدند.[۱۵]
فلسفه فارابی
از عصر فارابی تا عصر سبزواری، یعنی از قرن نهم تا نوزدهم میلادی، مبحث و مهمترین بحث تفکر اسلامی بود.[۱۶] فارابی به پیروی از ارسطو معتقد بود که جهان «قدیم» است. اما برای آنکه از چهارچوب تعلیمات قرآنی خارج نشود، سعی کرد بین عقیده ارسطو و مسئله خلق جهان در قرآن راهی بیابد. به همین سبب سعی میکرد موضوع «[۱۷] او معتقد است که «عقل فعال» ارسطو همان وحی قرآنی است.[۱۸]
فلسفه فارابی آمیزهای است از و نوافلاطونی که رنگ اسلامی و به خصوص شیعی اثنیعشری به خود گرفتهاست. او در منطق و اخلاق و سیاست، مابعدالطبیعه به مکتب فلوطینی گرایش دارد.
وحدت فلسفه
فارابی از کسانی است که میخواهند آراء مختلف را با هم وفق دهند. او در این راه بر همه گذشتگان خود نیز سبقت گرفت. او در این راه تا آن جا پیش رفت که گفت: فلسفه، یکی بیشتر نیست و حقیقت فلسفی - هر چند مکاتب فلسفی متعدد باشند - متعدد نیست.
فارابی به وحدت فلسفه سخت معتقد بود و برای اثبات آن براهین و ادله بسیاری ذکر کرد و رسائل متعدد نوشت که از آن جمله، کتاب «الجمع بین رایی الحکیمین افلاطون الالهی و ارسطو» به دست ما رسیدهاست.
وی معتقد بود که اگر حقیقت فلسفی واحد است، باید بتوان در میان افکار فلاسفه بزرگ به ویژه افلاطون و ارسطو توافقی پدید آورد. اساسا وقتی غایت و هدف این دو حکیم بزرگ، بحث دربارهٔ حقیقتی یکتا بودهاست، چگونه ممکن است در آراء و افکار، با هم اختلاف داشته باشند؟
فارابی میان این دو فیلسوف یونانی پارهای اختلافات یافته بود، اما معتقد بود که این اختلافات، اختلافاتی سطحی است و در مورد مسائل اساسی نیست. مخصوصاً آنکه آنها مبدع و پدیدآورندهٔ فلسفه بوده و همه حکمای بعدی کم و بیش، به این دو متکی هستند.
مسائلی که به عنوان اختلاف مبانی افلاطون و ارسطو مطرح بود و فارابی درصدد هماهنگ ساختن بین آنها برآمد، عبارت بودند از:
روش زندگی افلاطون و ارسطو، روش فلسفی افلاطون و ارسطو، نظریه یا تذکر، ، نظریه عادت.
البته تردیدی نیست که فارابی در این امر رنج بسیاری متحمل شده است؛ اما نکته مهم در این رابطه این است که یکی از منابع او برای انجام این مقصود، کتاب «
آثار فارابی
آثار فارابی از این قرار است:
-
۱) (آنچه شایستهاست قبل از فلسفه فرا بگیری): در این کتاب، فارابی منطق، هندسه، اخلاق نیکو و کنارهگیری از شهوات را پیش نیاز پرداختن به فلسفه ذکر میکند و دربارهٔ هر یک مطالبی بیان مینماید.
۲) (سیاست شهری): این کتاب دربارهٔ اقتصاد سیاسی است.
۴) (رسالهای دربارهٔ ماهیت و چیستی عقل): در این رساله اقسام عقول را تعریف و مراتب آنها را بیان میکند.
موضوع : تایپک کامپیوتر , تایپک علوم تجربی , تایپک اختر شناسی و نجوم , ,
امتیاز : نتیجه : امتیاز توسط نفر مجموع امتیاز :
بازدید : 1592 نويسنده: [cb:post_author_name] | [cb:post_create_date] ساعت [cb:post_create_time]

The Egyptian seked
The Egyptians defined the seked as the ratio of the run to the rise, which is the reciprocal of the modern definition of the slope.

Mathematicians of the Greco-Roman world
This map spans a millennium of prominent Greco-Roman mathematicians, from Thales of Miletus (c. 600 bc) to Hypatia of Alexandria (c. ad 400). Their names—located on the map under their cities of birth—can be clicked to access their biographies.

In the 4th century bc, Menaechmus gave a solution to the problem of doubling the volume of a cube. In particular, he showed that the intersection of any two of the three curves that he constructed (two parabolas and one hyperbola) based on a side (a) of the original cube will produce a line (x) such that the cube produced with it has twice the volume of the original cube.

Sphere with circumscribing cylinder
The volume of a sphere is 4πr3/3, and the volume of the circumscribing cylinder is 2πr3. The surface area of a sphere is 4πr2, and the surface area of the circumscribing cylinder is 6πr2. Hence, any sphere has both two-thirds the volume and two-thirds the surface area of its circumscribing cylinder.

Conic sections
The conic sections result from intersecting a plane with a double cone, as shown in the figure. There are three distinct families of conic sections: the ellipse (including the circle); the parabola (with one branch); and the hyperbola (with two branches).

Conchoid curve
From fixed point P, several lines are drawn. A standard distance (a) is marked along each line from line LN, and the connection of the points creates a conchoid curve.

Angle trisection using a conchoidNicomedes (3rd century
bce) discovered a special curve, known as a conchoid, with which he was able to trisect any acute angle. Given ∠θ, construct a conchoid with its pole at the vertex of the angle (
b) and its directrix (
n) through one side of the angle and perpendicular to the line (
m) containing one of the angle’s sides. Then construct the line (
l) through the intersection (
c) of the directrix and the remaining side of

Angle trisection using a hyperbolaPappus of Alexandria (
c.320) discovered that a hyperbola could be used to trisect an acute angle. Given ∠θ, construct points along one side such that
ba=
ao=
of, and draw the hyperbola with centre at
oand one vertex at
f. Next, construct the line perpendicular to side
basuch that
clies along the other side of ∠θ. Having established the length of
bc, draw the line
adsuch

Angle trisection using a hyperbolaPappus of Alexandria (
c.320) discovered that a hyperbola could be used to trisect an acute angle. Given ∠θ, construct points along one side such that
ba=
ao=
of, and draw the hyperbola with centre at
oand one vertex at
f. Next, construct the line perpendicular to side
basuch that
clies along the other side of ∠θ. Having established the length of
bc, draw the line
adsuch
mathematics, the science of structure, order, and relation that has evolved from elemental practices of counting, measuring, and describing the shapes of objects. It deals with logical reasoning and quantitative calculation, and its development has involved an increasing degree of idealization and abstraction of its subject matter. Since the 17th century, mathematics has been an indispensable adjunct to the physical sciences and technology, and in more recent times it has assumed a similar role in the quantitative aspects of the life sciences.
In many cultures—under the stimulus of the needs of practical pursuits, such as commerce and agriculture—mathematics has developed
موضوع : تایپک کامپیوتر , ,
امتیاز : نتیجه : امتیاز توسط نفر مجموع امتیاز :
بازدید : 1673 نويسنده: [cb:post_author_name] | [cb:post_create_date] ساعت [cb:post_create_time]
algorithm
algorithm, systematic procedure that produces—in a finite number of steps—the answer to a question or the solution of a problem. The name derives from the Latin translation, Algoritmi de numero Indorum, of the 9th-century Muslim mathematician al-Khwarizmi’s arithmetic treatise “Al-Khwarizmi Concerning the Hindu Art of Reckoning.”
For questions or problems with only a finite set of cases or values an algorithm always exists (at least in principle); it consists of a table of values of the answers. In general, it is not such a trivial procedure to answer questions or problems that have an infinite number of cases or values to consider, such as “Is the natural number (1, 2, 3, . . .) a prime?” or “What is the greatest common divisor of the natural numbers a and b?” The first of these questions belongs to a class called decidable; an algorithm that produces a yes or no answer is called a decision procedure. The second question belongs to a class called computable; an algorithm that leads to a specific number answer is called a computation procedure.
Algorithms exist for many such infinite classes of questions; Euclid’s Elements, published about 300 bc, contained one for finding the greatest common divisor of two natural numbers. Every elementary school student is drilled in long division, which is an algorithm for the question “Upon dividing a natural number a by another natural number b, what are the quotient and the remainder?” Use of this computational procedure leads to the answer to the decidable question “Does b divide a?” (the answer is yes if the remainder is zero). Repeated application of these algorithms eventually produces the answer to the decidable question “Is a prime?” (the answer is no if a is divisible by any smaller natural number besides 1).
Sometimes an algorithm cannot exist for solving an infinite class of problems, particularly when some further restriction is made upon the accepted method. For instance, two problems from Euclid’s time requiring the use of only a compass and a straightedge (unmarked ruler)—trisecting an angle and constructing a square with an area equal to a given circle—were pursued for centuries before they were shown to be impossible. At the turn of the 20th century, the influential German mathematician David Hilbert proposed 23 problems for mathematicians to solve in the coming century. The second problem on his list asked for an investigation of the consistency of the axioms of arithmetic. Most mathematicians had little doubt of the eventual attainment of this goal until 1931, when the Austrian-born logician Kurt Gödel demonstrated the surprising result that there must exist arithmetic propositions (or questions) that cannot be proved or disproved. Essentially, any such proposition leads to a determination procedure that never ends (a condition known as the halting problem). In an unsuccessful effort to ascertain at least which propositions are unsolvable, the English mathematician and logician Alan Turing rigorously defined the loosely understood concept of an algorithm. Although Turing ended up proving that there must exist undecidable propositions, his description of the essential features of any general-purpose algorithm machine, or Turing machine, became the foundation of computer science. Today the issues of decidability and computability are central to the design of a computer program—a special type of algorithm.
BibliographyHelp us expand the resources for this topic. Click below to submit new publication for review and accepted updates will be published to the site.WebsitesExternal WebsitesYou May Also Like...“I Didn't Know That...”موضوع : جبر و انالیز , منطق , ,
امتیاز : نتیجه : امتیاز توسط نفر مجموع امتیاز :
بازدید : 1251 نويسنده: [cb:post_author_name] | [cb:post_create_date] ساعت [cb:post_create_time]
يك سايت پر از مسئله و آموزش رياضيات.
http://www.risc.uni-linz.ac.at
اين سايت به مرکز تحقيقات محاسبات نمادين رياضي اختصاص دارد. انتشارات مؤسسه، تحقيقات انجام گرفته در اين مؤسسه درباره رياضيات، آموزش رياضيات، کاربردهاي صنعتي رياضيات، کاربرد کامپيوتر در رياضيات، راهنماي استفاده از نرمافزارهاي رياضي صنعتي و امکانات ثبت نام و عضويت در سايت را از عنوانهاي مندرج در سايت ميتوان برشمرد.
http://www.algebrahelp.com
اين سايت به نام راهنماي جبر به ارائه مطالب کمک آموزشي براي دانشآموزان و دانشجويان رشته رياضي در زمينه جبر ميپردازد. درسها، ماشينحساب، تمرين در منزل، حلالمسائل، ماشينحساب با امکانات حل معادلات جبري و بسياري مطالب ديگر درزمينه جبر را ميتوان در سايت مشاهده و از آنها استفاده نمود. مراجعه به اين سايت براي علاقمندان و دانشآموزان و دانشجويان رياضي توصيه ميگردد.
www.clifford.org/journals/jadvclfa.html
اين سايت به معرفي يک ژورنال تخصصي جبر به نام کليفورد ميپردازد. در اين ژورنال مطالبي درباره تازههاي جبر، کاربرد جبر در کامپيوتر و مطالب روز در اين زمينه ارائه ميشود. امکانات ثبت نام و عضويت در ژورنال فراهم آمده است، همچنين علاقمندان ميتوانند شمارههاي مختلف اين ژورنال را تحت فرمتهاي مختلف کامپيوتري از سايت دريافت نمايند.
http://www.perwass.de/CLU
در اين سايت به معرفي يک نرمافزار محاسباتي براي انجام محاسبات سه بعدي اجسام پرداخته ميشود. به کمک اين نرمافزار امکان دسترسي به نتايج کاملي از فرم رياضي در سطوح اجسام سه بعدي فراهم آمده است. اطلاعاتي درباره نرمافزار، پرسش و پاسخ و امکان Download نسخه آزمايشي نرمافزار در سايت فراهم آمده است.
www.walterpfeifer.ch/liealgebra
در اين سايت به ارائه اطلاعاتي درباره مؤسسه انتشاراتي رياضيات و فيزيک به نام Walter Pfeifer پرداخته ميشود. نام و موضوع کتب منتشر شده در اين مؤسسه درزمينه رياضي و فيزيک، عناوين اين سايت را شامل ميشوند.
http://vmoc.museophile.com/algebra
در اين سايت به ارائه تاريخچهاي از علم جبر و رياضيات از نگاه مرکز تحقيقات و آمار دانشگاه آکسفورد در جهان پرداخته ميشود. مطالبي درباره جبر، اصول رياضيات، آناليز جبري، آخرين روشهاي جبري، منابع اطلاعاتي رياضي و جبري، دايرةالمعارف جبر، موزه مجازي محاسبات جبري، رياضيدانان زن، دانشمندان و رياضيدانان، آموزش مطالب کمک آموزشي جبر، اکتشافات، روابط جبري و بسياري مطالب ديگر در اين زمينه را ميتوان از عنوانهاي مندرج در اين سايت نام برد.
http://www.vimagic.de/hope
تاريخچهاي بر معادلات و محاسبات در مسائل چند جملهاي رياضي عنوان انتخابي براي اين سايت ميباشد. تاريخچه، معادلات، هندسه فضايي و مطالب و مسائل در رياضيات چندجملهاي (کثير الجمله) عناوين مندرج در سايت را تشکيل ميدهند.
http://web.usna.navy.mil/~wdj/symm-gp.html
اين سايت را ميتوان به عنوان يک خودآموز براي نرمافزار تخصصي رياضي Maple5 عنوان کرد. در سايت به ارائه مطالب آموزشي و روشهاي حل مسائل رياضي با استفاده از اين نرمافزار پرداخته شده است. علاقمندان به اين نرمافزار ميتوانند با مراجعه به اين سايت از اطلاعات مندرج در آن براي فراگيري اين نرمافزار بهره برند.
http://joshua.smcvt.edu/linearalgebra
در اين سايت به ارائه يک کتاب الکترونيکي آموزش جبرخطي پرداخته شده است. در اين سايت علاوه بر کتاب فوق ميتوان اطلاعاتي درباره ماهيت جبرخطي و نويسنده کتاب را در اختيار داشت.
http://www.numbertheory.org/book
در اين سايت کتابي تحت عنوان جبرخطي مقدماتي به صورت الکترونيکي ارائه ميگردد. فصلهاي مختلف کتاب به صورت فهرست در سايت آمدهاند که ميتوان با استفاده از آنها به مطالب مورد نظر دسترسي پيدا کرد.
امتیاز : نتیجه : امتیاز توسط نفر مجموع امتیاز :
بازدید : 1664 نويسنده: [cb:post_author_name] | [cb:post_create_date] ساعت [cb:post_create_time]
5 دزد دریایی با سن های مختلف، صندوقی شامل 100 سکه طلا به دست می آورند و قصد تقسیم آنرا دارند.روش تقسیم به این صورت است که مسن ترین آنها طرحی برای تقسیم ارائه می کند، سپس هر 5 نفر به این طرح رای می دهند. اگر 50% یا بیشتر رای مثبت به دست آید طرح اجرا می شود وگرنه شخص ارائه کننده ی طرح را به دریا می اندازند. و این کار با نفر بعدی که مسنتر است تکرار میشود.
چون این دزدان سعی می کنند رقیب را حذف کنند، پس اگر رای مثبت یا منفی هر یک از آنها تاثیری در سهمش نداشته باشد حتما رای منفی می دهید. با توجه به اینکه هرکدام می خواهند بیشترین سهم را داشته باشند و نمی خواهند به دریا انداخته شوند، در پایان سکه ها به چه روشی تقسیم میشوند؟
امتیاز : نتیجه : امتیاز توسط نفر مجموع امتیاز :
بازدید : 1540 نويسنده: [cb:post_author_name] | [cb:post_create_date] ساعت [cb:post_create_time]
آنچه که تناقض آمیز، باورنکردنی یا خلاف انتظار (و شهود) ماست.(آنچه به نظر درست می رسد ولی غلط است، به نظر غلط می رسد ولی درست است، یا به نظر غلط می رسد و واقعا غلط است. )
فایده پارادوکسها
)ایجاد انگیزه برای گسترش مرزهای دانش؛
)تعمیق بینش؛
)تعمیم شیوه های استدلال؛
)افزایش دقت؛
)وضع قوانین زبان شناختی جدید.
بعضی پارادوکسها که متضمن تناقض اند صادق به نظر می رسند وحتی این ایده را به ذهن نزدیک می کنند که چرا تناقضها را نپذیریم!درمنطق پیراسازگار (paraconsistent) می توان تناقض داشت و بر خلاف ریاضیات کلاسیک، چنین نیست که از تناقض هر چیزی نتیجه شود.
پارادوکس روز تولد
اگر نفر در این سخنرانی شرکت کرده باشند، احتمال این که حداقل نفر روز تولدشان یکی باشد حدود % است، اگر نفر شرکت کرده باشند این احتمال حدود /% و اگر بیش از نفر حضور داشته باشند این عدد بزرگتر از % است.
پاردوکسهای زنون Zenos Paradoxes
در صورتی که پاره خط بینهایت بار تقسیم پذیر باشد، حرکت ناممکن است، زیرا برای این که پاره خطی مانند ABرا با شروع از نقطه A بپیماییم،
ابتدا باید به نقطة وسط آن Cبرسیم. برای این که ACپیموده شود، باید به نقطة وسط آن D برسیم و قس علیهذا. پس نمی توان حتی از نقطة A حرکت کرد. A---D---C-------B
در مسابقه دو بین آشیل تندرو و لاک پشت کندرو، آشیل که کمی عقب تر از لاک پشت است، هیچگاه به او نمی رسد. زیرا ابتدا باید به نقطه ای برسد که لاک پشت از آنجا حرکت کرده است. اما وقتی به آنجا می رسد لاک پشت قدری جلوتر رفته است و همان وضعیت قبل روی می دهد و با تکرار این روند، گرچه آشیل به لاک پشت نزدیک می شود ولی هیچگاه به او نمی رسد. A------------T------
پارادوکس لامپ تامسون (Tompson Lamp Paradox )
لامپی به مدت یک دوم دقیقه روشن می شود، سپس برای یک چهارم دقیقه خاموش می شود، به مدت یک هشتم دقیقه روشن میشود و قس علیهذا. درست بعد از یک دقیقه لامپ روشن خواهد بود یا خاموش؟
پارادوکس دار غیرمنتظره ( Unexpected Hanging Paradox )
به یک زندانی گفته می شود که او در یکی از روزهای بین شنبه و پنجشنبه به دار آویخته خواهد شد، اما تا روز به دار آویخته شدن، وی نخواهد دانست که کدام روز اعدام می شود.او روز پنجشنبه به دار آویخته نمی شود، زیرا اگر او تا چهارشنبه زنده باشد می فهمد که اعدام در روز پنحشنبه صورت خواهد گرفت، اما به او گفته شده است که وی از روزی که به دار کشیده می شود پیشاپیش آگاه نیست. او روز چهارشنبه نیز اعدام نمی شود زیرا اگر تا سه شنبه زنده بماند، با توجه به این که بنا به استدلال بالا روز پنجشنبه اعدام نمی شود، می فهمد که روز چهارشنبه اعدام انجام خواهد شد. استدلال مشابه نشان می دهد که او در هیچیک از روزهای دیگر نیز نمی تواند اعدام شود.اما در روزی غیر از پنجشنبه جلاد وارد می شود و وی را اعدام می کند.
پارادوکس توده ( Sorites Paradox )
یک دانة گندم یک تودة گندم نیست. با اضافه کردن یک دانه گندم، به دو دانه دست می یابیم که باز هم تودة گندم نیست. با اضافه کردن یک دانه گندم دیگر، سه دانه گندم خواهیم داشت که توده محسوب نمی شود. اگر این عمل را تکرار کنیم، هیچگاه به تودة گندم نمی رسیم.اما زمانی که این گردایة گندم به قدر کافی بزرگ شود، توده نامیده می شود.
پارادوکس ریچارد (Jules Richard's Paradoxesَ)
آیا کوچکترین عدد طبیعی که نتوان آن را با کمتر از صد حرف فارسی نمایش داد وجود دارد؟ چون تعداد اعداد طبیعی نا متناهی و تعداد حروف فارسی متناهی است پس عددی وجود دارد که نمی توان آن را با عبارتی شامل کمتر از صد حرف فارسی تعریف کرد. بنا به اصل خوش ترتیبی در اعداد طبیعی، کوچکترین عدد طبیعی که نتوان آن را با کمتر از صد حرف فارسی نمایش داد وجود دارد. اما عبارت بالا که بین دو نماد و قرار دارد کمتر ار صد حرف ( یعنی پنجاه و سه حرف ) دارد، یعنی عدد ارائه شده با کمتر از صد حرف فارسی تعریف شد!
پارادوکس خداوند قادر مطلق
آیا خداوند می تواند سنگی بسازد که نتواند بلند کند؟
پارادوکس اژدها
چگونه می توانیم راجع به چیزی که وجود ندارد صحبت کنیم، وقتی که می گوییم اژدهای هفت سر وجود ندارد.
پارادوکس تخته سیاه
تخته سیاهی را در نظر بگیرید که روی آن علاوه بر اعداد ، ، ، جملة کوچکترین عدد طبیعی که روی این تخته سیاه ارائه نشده است. نوشته شده است.
در این صورت گرچه عدد روی تخته سیاه نمایش داده نشده است، ولی عبارت مذکور روی تخته سیاه، مبین است.
پارادوکس بوچوفسکی ( Buchowski Paradox )
فرض کنید شما فقط دو برادر دارید که هر دو از شما مسن تر هستند. در این صورت جملة به ظاهر غلط ذیل، راست است:
برادر جوانترم از من مسن تر است
پارادوکس دروغگو( Liar's Paradox) یا پارادوکس ائوبولیدس (Eubulides' Paradox )
می گویند روزی ائوبولیدس، متفکر یونانی قرن چهارم قبل از میلاد، گفت: چیزی که آلان می گویم دروغ است. اگر گفتة او درست باشد، آنگاه بنا به آنچه گفته است، باید گفته اش دروغ باشد، واگر گفتة او دروغ باشد، دوباره بنابر آنچه گفته است نتیجه می شود که گفته اش درست است.
پارادوکس دور
این پارادوکس توسط آلبرت ساکسونی در قرون وسطی طرح گردیده است:
جملة P این است: q دروغ است.
جملة q این است: P راست است.
نکته جالب این است که اگر ما دارای یک نوع منطق سه ارزشی باشیم که در آن گزاره ها بتوانند فقط یکی از ارزشهای راست، دروغ و نه راست ـ نه دروغ را داشته باشند آنگاه گزارةP به صورت P دروغ یا نه راست ـ نه دروغ است نمی تواند هیچیک از ارزشهای راست ، دروغ و نه راست نه دروغ را به خود بگیرد.
پارادوکس تابلو
این پارادوکس در توسط ریاضیدان انگلیسی جردن (P. E. B. Jourdain) ارائه شد:
تابلوئی داریم که در یک طرف آن
جمله پشت این تابلو راست است. و در طرف دیگر آن جمله پشت این تابلو دروغ است. نوشته شده است!
پارادوکس سقراط ( Socrates Paradox )
نقل شده است که ســـــقراط روزی گفته است: چیزی که می دانم این اسـت که من هیـچ چیز نمی دانم .
پارادوکس جزیرة وحشی ها
در جزیره ای قبیله ای وحشی زندگی می کردند که دو خدا، خدای راستی و خدای دروغ داشتند. آنها هر کس را که به جزیره می آمد قربانی می کردند، به این ترتیب که از وی سوالی می پرسیدند، اگر راست می گفت او را قربانی خدای راستی و اگر دروغ می گفت، او را قربانی خدای دروغ می کردند. روزی شخصی وارد جزیره شد. او را گرفتند و از او پرسیدند سرنوشت تو چه خواهد بود؟ آن شخص جواب داد شما من را قربانی خدای دروغ خواهید کرد. با این جواب وحشی ها مستاصل شدند زیرا خواه راست گفته باشد و خواه دروغ باید هم قربانی خدای راستی شود و هم قربانی خدای دروغ!
پارادوکس آرایشگر ( Barber Paradox) یا پارادوکس راسل (Russells Paradox )
در دهکده ای فقط یک آرایشگر وجود دارد. او فقط ریش کسانی را می تراشد که ریش خود را نمی تراشند. سوال این است که ریش خود ریش تراش را چه کسی می تراشد؟ اگر او ریش خود را نتراشد، باید نزد ریش تراش یعنی خودش، برود تا ریشش را بتراشد و اگر ریش خود را بتراشد، نباید توسط ریش تراش یعنی خودش، ریشش تراشیده شود.
پارادوکس فهرست ( Catalogue Paradox )
کتابداری در حال تدوین یک فهرست کتابشناسی از تمام فهرستهای کتابشناسی و تنها آنهایی است که نام خود را در فهرست ذکر نکرده اند. آیا فهرست این کتابدار، نام خودش را نیز در بر می گیرد؟
پارادوکس خود نا توصیف ( Heterological Paradox )
خود ناتوصیف، کلمه ای است که خودش را توصیف نمیکند. پس کلمة خود ناتوصیف خود ناتوصیف است اگر و فقط اگر خود ناتوصیف نباشد.
پارادوکس اسمارانداچ (Smarandache Paradox )
فرض کنید A یکی از عبارات ممکن، کامل و . . . باشد. در این صورت همه چیز A است ایجاب می کند که ~A نیز A باشد. مثلاً وقتی می گوییم همه چیز ممکن است ، نتیجه می شود که غیر ممکن نیز ممکن است ، یا از هیچ چیز کامل نیست این که کامل نیز کامل نیست مستفاد می شود.
پارادوکس کانتور( Cantor's Paradox )
فرض کنید Aمجموعه همة مجموعه ها باشد، پسP(A)=A و لذا ( card(P(A))=card(A از طرفی بنا به قضیة کانتور( card(P(A))< P>
پارادوکس نیوکام
فرض کنید دو جعبه A و B داده شده باشد. سر جعبه A باز و سر جعبه B بسته باشد. A شامل دلار و B شامل دلار است و یا شامل هیچ چیز نیست. شما باید فقط جعبه B را انتخاب کنید و یا هر دو جعبه A و B را. اما قبل از این که شما انتخاب خود را انجام دهید، پیشگویی بر اساس انتخابی که شما انجام خواهید دا د در جعبه B ، د اگر شما فقط جعبه B را انتخاب کنید و هیچ چیز نمی گذارد اگر شما هر دو جعبه A وB را انتخاب کنید.
سوال: اگر شما به انتخاب فقط B تمایل داشته باشید، می توانید A را نیز انتخاب کنید؟
امتیاز : نتیجه : امتیاز توسط نفر مجموع امتیاز :
بازدید : 2037 نويسنده: [cb:post_author_name] | [cb:post_create_date] ساعت [cb:post_create_time]
تلفن هوشمند خود را با پدال زدن شارژ کنید
اکوایکس پاور دوچرخهای است که انرژی حرکتی پدال دوچرخه را به الکتریسته تبدیل کرده تا بتوان از آن برای شارژ کردن تلفنهای هوشمند یا دستگاههای مشابه استفاده کرد.
اکوایکس پاور دوچرخهای است که انرژی حرکتی پدال دوچرخه را به الکتریسته تبدیل کرده تا بتوان از آن برای شارژ کردن تلفنهای هوشمند یا دستگاههای مشابه استفاده کرد.
تاکنون محصولات فناورانه مختلفی ساخته شده که میتواند انرژی حرکتی را به انرژی الکتریسته تبدیل کند اما این دوچرخه به واسطه شارژ کردن تلفن همراه یا دستگاه موقعیتیاب ماهوارهای و فراهم کردن انرژی الکتریسیته برای نورهای جلویی به طور همزمان خود را با سایر محصولات از این دست متمایز کرده است.
این محصول فناوری اکوایکس پاور دو ساختار مهم را تغییر داده است، فرمان دوچرخه منطبق شده با صفحه لمسی و بدنه ضد آب که دربرگیرنده تلفنهای هوشمند آیفون، آندروید، ویندوز، بلکبری، دستگاههای پخش موسیقی و اکثر مدلهای GPSها است که به چرخ جلو متصل میشود.
یک دستگاه دینام که از کلاج برای ارتباط با حرکتهای چرخ و تبدیل انرژی حرکتی به الکتریسیته استفاده میکند نیز به چرخ متصل است و هر دو ساختار با یک کابل به هم وصل شدهاند. بدنه اصلی این دستگاه دربرگیرنده یک چراغ جلو و یک چراغ عقب است که هرکدام از آنها با LED روشن میشود و توسط یک کلید روشن/خاموش که در فرمان دوچرخه قرار گرفته کنترل میشود.
چراغهای عقب و جلوی دوچرخه نور خود را از یک باتری لیتیوم – یون 700 mAh تامین میکند که چراغها و شارژ را تا 5/1 ساعت بدون پدال زدن روشن نگاه میدارد تا از این امر اطمینان داشته باشید که اگر در ترافیک مسیر بمانید چراغهای دوچرخه در زمان شب خاموش نمی شوند. این دوچرخه از سوی شرکت اکوایکس گیر با قیمت 99/99 دلار عرضه شده است.امتیاز : نتیجه : امتیاز توسط نفر مجموع امتیاز :
بازدید : 1449 نويسنده: [cb:post_author_name] | [cb:post_create_date] ساعت [cb:post_create_time]
مهندسی مکانیک شاخهای از مهندسی است که با طراحی، ساخت و راهاندازی دستگاهها و ماشینها سروکار دارد. همچنین این رشته در ارتباط نزدیک با ماشینهایی است که کارهای متنوع بسیار و یا تبدیل انرژیهای مختلف نظیر انرژی خورشید، انرژی هستهای و انرژی شیمیایی را به انرژی حرکتی انجام میدهند. مهندسی مکانیک نقش بسزایی در بالا بردن امنیت زندگی، بهبود کیفیت کلی زندگی، و نیز ایجاد شور و نشاط اقتصادی ایفا میکند. مهندسی مکانیک در نقش زمینهای برای سایر علوم فیزیکی میباشد. به جرات میتوان گفت که مهندسی مکانیک گستردهترین رشتهٔ مهندسی از نظر دامنهٔ فعالیتها و کاربردها است.
مهندسان مکانیک، اصول اساسی نیرو، انرژی، حرکت و گرما را به کار برده و با دانش تخصصی خود، سیستمهای مکانیکی و دستگاهها و فرآیندهای گرمایی را طراحی کرده و میسازند. مهندسان مکانیک، گسترهٔ وسیعی از دستگاهها، فرآوردهها و فرآیندها را تولید میکنند؛ به عنوان نمونه:
موتورها و سیستمهای کنترل خودرو و هواپیما، نیروگاههای الکتریکی، دستگاههای پزشکی، اجزا و قطعههای گوناگون از موتورهای با ابعاد میکروسکوپی گرفته تا چرخدندههای غولآسا، فناوری لیزر، طراحی و ساخت به کمک رایانه، ماشینی کردن یا خودکارسازی (اتوماسیون) و روباتیک، انواع گوناگونی از فرآوردههای مصرفی از دستگاههای تهویهٔ مطبوع گرفته تا رایانههای شخصی و تجهیزات ورزشی، ماشینها و دستگاههایی که هر یک از فرآوردههای بالا را به صورت انبوه تولید میکنند.میتوان گفت تقریباً همهٔ جنبههای زندگی، در ارتباط با مهندسی مکانیک هستند. هر چیزی که حرکت کند یا انرژی مصرف نماید، احتمالاً یک مهندس مکانیک در طراحی یا ساخت آن نقش داشته است.
محتویات
مهندسان مکانیک معروف
چند تن از مهندسان مکانیک معروف که پیش از این میزیستهاند، عبارتاند از:
- (۱۸۴۴-۱۹۲۹): مخترع موتورهای دیزلی و بنیان گذار موتورهای احتراق داخلی ( هم دوره با دایملر و می باخ)و سازنده اولین خودروی تجاری، مبدع پدال گاز در خودرو و سیستم جرقه زنی با استفاده از شمع و باتری، مخترع کلاچ و مکانیزم تعویض دنده، کاربراتور و رادیاتور نیز از اختراعات اوست.
- (۱۸۳۴-۱۹۰۰): مهندس و طراح صنعتی، به همراه می باخ مخترع اولین موتور سیکلت (دوچرخه موتور دار)و پیشرو در گسترش موتورهای احتراق داخلی، پدر بزرگ موتورهای احتراق داخلی.
- (۱۹۰۶-۱۹۶۸): دستگاه زیراکس از نوآوریهای اوست.
- (۱۸۱۴-۱۸۶۲): سازندهٔ اسلحهٔ کولت.
- (۱۹۰۶-۱۹۹۱): بنیانگذار شرکت معروف هوندا.
- (سینجر) (۱۸۱۱-۱۸۷۵): سازندهٔ نخستین چرخ خیاطی خانگی.
- آلفرد برنارد نوبل: پایهگذار اندیشهٔ جایزهٔ نوبل.
- رودولف دیزل: سازندهٔ موتورهای معروف دیزل که با گازوئیل کار میکنند.
- ویلیس کریر: مخترع تهویه مطبوع
- :در زمینه مبدلهای حرارتی خدمات ارزندهای بر جای نهاد و مولف کتاب heat exchanger design نیز میباشد.
- (۱۸۴۶-۱۹۲۹):مهندس و طراح صنعتی، صاحب نشان میباخ، همکاری با دایملر در ساخت موتورهای احتراق داخلی و موتورهای چهار زمانه، دارنده دکترای افتخاری از دانشگاه اشتوتگارت، عضو افتخاری انجمن مهندسین آلمان.
- نیکلاس اتو(۱۸۳۲-۱۸۹۱):مهندس ومخترع اولین موتور احتراق داخلی با بازدهی مطلوب، تعمیم دهنده مفهوم چهار زمانه به موتورهای احتراق داخلی.
- جیمز وات: تکمیل کننده موتور بخار و پدر انقلاب صنعتی
زمینههای فعالیّت در مهندسی مکانیک
زمینههای فعالیّت مهندسی مکانیک به طور جامعتر عبارتاند از:
- در زمینهٔ طراحی:
- ماشینها و دستگاههایی که هر نوع محصولی را ساخته و بستهبندی میکنند.
- تجهیزات گردنده مانند پمپها، فشردهسازها (کمپرسورها)، دمندهها، توربوماشینها (توربینها و ...).
- موتورهای درونسوز
- مخزنهای تحت فشار، رآکتورها، مبادلهکنهای گرمایی، دیگهای بخار
- سامانههای لولهکشی
- وسیلههای نقلیه مانند خودرو، کامیون، اتوبوس، هواپیما، قطار و ...
- تجهیزات حمل مواد مانند تسمهنقّالهها، روباتها و ...
- طراحی کنترلر برای سیستمهای دینامیکی
- طراحی سیستمهای تهویه مطبوع و گرمایش و سرمایش در ساختمان ها
- در زمینهٔ تحلیل:
- شکست دستگاهها
- بهبود عملکرد و قابلیّت اطمینان
- انتقال گرما
- ارتعاشات مکانیکی، آکوستیک
- پیزوالکتریک
- در زمینهٔ آزمایش:
- آزمایش کیفیّت، امنیّت و قابلیّت اطمینانِ فرآوردهها، دستگاهها و فرآیندها
- در زمینه فرآیندهای ساخت و تولید
- فرایندهای ماشینکاری سنتی
- فرایندهای ماشینکاری غیر سنتی
- فرایندهای شکلدهی شامل شکلدهی ورقی و حجمی
- طراحی و ساخت قالبها و قیود
- روشهای اتصال و جوشکاری
- عملیات حرارتی
- روشهای ریخته گری
- مترولوژی و سیستمهای اندازه گیری
- زمینههای نوین
- فن آوری نانو
- سیستمهای میکروالکترومکانیکی (حسگری و عملگری)
- سیستمهای دارو رسانی در ابعاد نانو
- سیستمهای میکرو و نانو سیالاتی
- نانو روباتها
- همکاری با مهندسان دیگر رشتهها (مانند مهندسی عمران، برق، شیمی و ...) به منظور طراحی واحدهای تولیدکنندهٔ انواع گوناگون فرآوردهها
آینده شغلی مهندسی مکانیک
چشمانداز شغلی مهندسان مکانیک، امیدبخش و بااستحکام است. برای مثال، در ایالات متحد آمریکا، رشد شغلها و حرفههای مربوط به مهندسی مکانیک، هر سال حدود ۱۶٪ (۳۵ هزار شغل) است و انتظار میرود این آهنگ رشد تا سالهای آینده حفظ شود. مهندسان مکانیک از روزگاران گذشته تا به امروز، اغلب در بخشهای صنعتی زیر نقش عمدهای ایفا میکنند:
هوا فضا، خودروسازی، واحدهای شیمیایی، فن آوری نانو، رایانه و الکترونیک، ساختمانسازی، انواع فرآوردههای مصرفی، انرژی، مشاوره مهندسی و بخشهای دولتی.
همچنین صنعت پزشکی و داروسازی، فرصتهای شغلی هیجانانگیزی را برای مهندسان مکانیک به وجود آوردهاند تا نیروها و دانشهای زیستی را در هم بیامیزند. همچنین فرصت شغلی این رشته در ایران نسبت به رشتههای دیگر بسیار مناسب است.گرایشهای مهندسی مکانیک در دانشگاههای ایران
- گرایشهای عمومی
- مکانیک - طراحی جامدات (فعالیت در طراحی ماشین آلات صنعتی، خطوط تولید کارخانجات، طراحی سیستمهای انتقال نیرو و...)
- مکانیک - حرارت و سیالات (فعالیت در زمینهٔ طراحی موتورهای احتراق داخلی، موتورهای جت، بررسیهای ایرودینامیکی، هوافضا، طراحی سیستمهای هیدرولیکی و پنوماتیکی، نیروگاههای حرارتی و برودتی و پالایشگاههای نفت و تاسیسات مکانیکی ساختمان و...)
- مکانیک - ساخت و تولید (فعالیت در کارگاههای قالب سازی، ابزارسازی، جوشکاری و ساخت و تولید ماشین الات صنعتی و...)
- گرایشهای خاص
- مکانیک - دریا
- مکانیک - تأسیسات (فعالیت در زمینه سیستمهای گرمایشی و سرمایشی و تهویه مطبوع و آتش نشانی و... ساختمانها)
- مکانیک - نیروگاه و انرژی
- مکانیک - مهندسی خودرو
- مکانیک - ماشین آلات کشاورزی
- مکانیک - نیروگاه
- مکانیک - نگهداری و تعمیرات
مباحث اساسی در مهندسی مکانیک
مبحثها و موضوعهای اساسی مهندسی مکانیک عبارتاند از:
- ایستاییشناسی (استاتیک)
- پویاییشناسی (دینامیک)
- مکانیک مادهها (مقاومت مصالح)
- ترمودینامیک مهندسی
- مکانیک شارهها (مکانیک سیالات)
- دینامیک سیّالات
- انتقال گرما (انتقال حرارت)
- نظریهٔ کنترل
- سیستمهای کنترل شامل:
مهمترین نرمافزارهای مورد استفاده در مهندسی مکانیک
- Adams
- LS-DYNA
- AUTODYN
- pro-engineer پرو/اینجینیر(نرمافزار طراحی قطعات)
- Marc (نرمافزار تحلیل نیروها و تنشها)
- Ansys نرمافزاری برای تحلیل مهندسی قطعات در تحلیلهای دینامیکی
- CAD نرمافزار طراحی ۲d و۳d
- کتیا (نرمافزار طراحی قطعات)
- Gambit(نرم فزاری برای مدلسازی و ایجاد مدل ریاضی برای حل گر فلوئنت)
- MasterCAm (تولید به کمک کامپیوتر)
- Fluent (نرم افزار شبیه سازی حرکت سیالات ویا به عبارتی حل معادلات مومنتوم به صورت عددی )
- متلب (نرمافزاری برای نوشتن برنامه و محاسبات ریاضی در مهندسی)
- متکد
- Working Model
- Nastran
- PATRAN
- آباکوس
- سالیدورکس (نرمافزار طراحی قطعات)
- اتوکد (نرمافزار طراحی قطعات)
- inventor
- Mechanical Desktop
- Microstation
- افرا (نرمافزار محاسبات ریاضی و مهندسی)
- CadPipe
- Power shape نرمافزار مدلسازی
- Power mill نرمافزار شبیه سازی تولید قطعات
- PDMS
- PDS
- AutoPipe
- AutoPlant
- EES (Engineering Equation Solver)
- Carrier نرم افزار قدرتمند طراحي سيستم هاي تهويه مطبوع از شركت كرير آمريكا
- Aspen B-Jac
- Aspen HTFS
- PVElite (نرم افزار طراحی مخازن تحت فشار)
- building systems
- Cosmos (نرمافزار تحلیل نیروها و تنشها)
- POWERMILL&POWERSHAPE
- CAESAR II
- ++FLO
- CODECALC
- TANK
امتیاز : نتیجه : امتیاز توسط نفر مجموع امتیاز :
برچسب ها : مهندسی مکانیک , ,
بازدید : 1386 نويسنده: [cb:post_author_name] | [cb:post_create_date] ساعت [cb:post_create_time]
ابو موسی جابر بن حیان (زادهٔ سال ۱۰۰ هجری شمسی معادل با ۷۲۱ میلادی در توس - درگذشتهٔ سال ۱۹۴ هجری شمسی معادل با ۸۱۵ میلادی در کوفه[۱]) دانشمند و کیمیاگر و فیلسوف شیعه ایرانی[۲] [۳][۴][۵] بود. او را «پدر علم شیمی» نامیدهاند و بسیاری از روشها (مانند تقطیر) و انواع ابزارهای اساسی شیمی مانند قرع و انبیق را به او نسبت میدهند. پژوهشگران بر این باورند که زادگاه او شهر توس در خراسان ایران بودهاست.
محتویات
زندگی
ابو موسی، جابر بن حیان، کیمیاگر برجستهٔ ایرانی، در سال صد هجری شمسی در شهر توس از توابع خراسان متولد شد. مدت کوتاهی پس از تولدش، پدر او که یک داروساز شناخته شده و پیرو مذهب شیعه بود، به دلیل نقشی که در بر اندازی حکومت اموی داشت، دستگیر شد و به قتل رسید. جابر به نوشتههای باقی مانده از پدرش علاقه مند شد و به ادامهٔ حرفهٔ او پرداخت. او با شوق و علاقه به یادگیری علوم دیگر نیز میپرداخت. همین، سبب هجرت او از ایران به عراق شد. گر چه بعضیها گفتهاند که جابر نزد جعفر صادق (امام ششم شیعیان) علمآموزی کرده است اما تحقیقات نشان داده است که این امر غیر ممکن بوده است.[۶] کتابها و رسالات متعدد جابر، سالها بعد از او، توجه کیمیاگران اروپایی را به خود جلب کرد. آنها این کتابها را به زبان لاتین ترجمه کردند و سالها از آن به عنوان منبع معتبری استفاده میکردند. به گفتهٔ آنها، این کتابها تاثیر عمیقی بر تغییر و تصحیح دیدگاه کیمیاگران غربی گذاشتهاست. عاقبت، جابر بن حیان، در سال صد و نود و چهار ه.ش (معادل با ۸۱۵ میلادی) در شهر کوفهٔ عراق چشم از جهان فروبست. به اتفاق پژوهشگران بر این باورند که صفت کوفی که در روایات بسیاری به دنبال نام جابر آمدهاست، نشانگر زادگاه او نیست، بلکه حاکی از آن است که وی مدتی در کوفه اقامت داشتهاست.
اختلاف نظر در مورد تاریخ تولد وی
در مورد تاریخ دقیق تولد و مرگ و محل تولد وی اختلاف نظر وجود دارد. به گفتهٔ برخی وی متولد سال ۱۰۰ هجری شمسی و وفات وی در سال ۱۹۴ هجری شمسی بوده است.[۷] برخی نیز او را متولد سال ۱۰۳ هجری شمسی دانسته و وفات وی را در سال ۲۰۰ هجری شمسی ذکر کردهاند.[۸] با این حال دانشنامهٔ بریتانیکا وی را متولد سال ۷۲۱ میلادی و وفات وی را در سال ۸۱۵ میلادی (نزدیک به هزار و دویست سال پیش) ثبت کرده است.[۳]
منزلت جابر در علم شیمی
جابر نخستین شیمیدان ایرانی است. وی اولین کسی است که به علم شیمی شهرت و آوازه بخشید و بیتردید نخستین مسلمانی است که شایستگی کسب عنوان شیمیدان را دارد. بعضی عقیده بر این دارند که وی عرب بوده اما اینطور نبودهاست. ظاهراً همین بلندی مقام، پرآوازگی و دانش عظیم او موجب شدهاست که بعضی او را مورد قدردانی و ستایش و بعضی دیگر مورد حسادت و کینهتوزی خود قراردهند.
اکسیر و عقیده جابر درباره آن
عقیده جابراین بود همچنان که طبیعت میتواند اشیا را به یکدیگر تبدیل کند، مانند تبدیل خاک و آب به گیاه و تبدیل گیاه به موم و عسل بهوسیله زنبور عسل و تبدیل قلع به نقره در زیر زمین و … کیمیاگر نیز میتواند با تقلید از طبیعت و استفاده از تجربهها و آزمایشها همان کار طبیعت را در مدت زمانی کوتاهتر انجام دهد. اما کیمیاگر برای اینکه بتواند یک شیء را به شیء دیگر تبدیل کند، بهوسیلهای نیازمند است که اصطلاحاً آن را اکسیر مینامند.
اکسیر در علم کیمیا، به منزله دارو در علم پزشکی است. جابر اکسیر را که از آن در کارهای کیمیایی خود استفاده میکرد، ازانواع موجودات سه گانه (فلزات، حیوانات و گیاهان) به دست میآورد. او خود، در این زمینه میگوید: هفت نوع اکسیر وجود دارد:
- اکسیر فلزی: اکسیر بدست آمده از فلزات.
- اکسیر حیوانی: اکسیر بدست آمده از حیوانات.
- اکسیر گیاهی: اکسیر بدست آمده از گیاهان.
- اکسیر حیوانی - گیاهی: اکسیر بدست آمده از امتزاج مواد حیوانی و گیاهی.
- اکسیر فلزی - گیاهی: اکسیر بدست آمده از امتزاج موادفلزی و گیاهی.
- اکسیر فلزی - حیوانی: اکسیر بدست آمده از امتزاج مواد فلزی و حیوانی.
- اکسیر فلزی - حیوانی - گیاهی: اکسیر بدست آمده از امتزاج مواد فلزی و گیاهی و حیوانی.
نگارخانه ابزار کیمیاوی
عقیده جابر درباره فلزات
فلزات اصلی هفت تا است: طلا، نقره، مس، آهن، سرب، جیوه و قلع
این فلزات به تعبیر جابر اساس صنعت كيميا را تشکیل میدهند. به عبارت دیگر قوانین علم کیمیا بر این هفت فلز استوار است. با این حال، خود این کانیها از ترکیب دو کانی اساسی، یعنی گوگرد و جیوه بوجود میآیند که به نسبتهای مختلف، در دل زمین، باهم ترکیب میشوند. بنابراین، تفاوت میان فلزات هفتگانه تنها یک تفاوت عرضی وجود دارد نه جوهری که محصول تفاوت نسبت ترکیب گوگرد و جیوه در آن است. اما طبیعت هر یک از گوگرد و جیوه تابع دو عامل زمینی و زمانی است. به عبارت دیگر، تفاوت خاک زمینی که این دو کانی در آن بوجود میآیند و همچنین تفاوت وضعیت کواکب به هنگام پیدایش آنها موجب میشود که طبیعت گوگرد و یا جیوه تفاوت پیدا کند.
تعریف جابر از بعضی فلزات و تبدیل آنها
- قلع
دارای چهار طبع است. ظاهر آن، سرد و تر و نرم و باطنش گرم و خشک و سخت … پس هرگاه صفات ظاهر قلع به درون آن برده شود و صفات باطنی آن به بیرون آورده شود، ظاهرش خشک و در نتیجه قلع به آهن تبدیل میشود.
- آهن
از چهار طبع پدید آمدهاست که از میان آنها، دو طبع، یعنی حرارت و خشکی شدید به ظاهر آن اختصاص دارد و دو طبع دیگر یعنی برودت و رطوبت به باطن آن. ظاهر آن، سخت و باطن آن نرم است. ظاهر هیچ جسمی به سختی ظاهر آن نیست. همچنین نرمی باطن آن به اندازه سختی ظاهرش است. از میان فلزات جیوه مانند آهن است. زیرا ظاهر آن آهن و باطن آن جیوهاست.
- طلا
ظاهر آن گرم و تر و باطنش سرد و خشک است. پس جمیع اجسام (فلزات) را به این طبع برگردان. چون طبعی معتدل است.
- زهره(=مس)
گرم و خشک است ولی خشکی آن از خشکی آهن کمتر است زیرا طبع اصلی مس، همچون طلا، گرم و تر بودهاست اما در آمدن خشکی بر آن، آن را فاسد کردهاست. لذا با از میان بردن خشکی، مس به طبع اولیه خود برمیگردد.
- جیوه
طبع ظاهری آن سرد و تر و نرم و طبع باطنیاش گرم و خشک و سخت است. بنابراین ظاهر آن، همان جیوه و باطنش آهن است. برای آن که جیوه را به اصل آن یعنی طلا برگردانی، ابتدا باید آن را به نقره تبدیل کنی.
- نقره
اصل نخست آن، طلا است ولی با غلبه طبایع برودت و یبوست، طلا به درون منتقل شدهاست و در نتیجه ظاهر فلز، نقره و باطن آن طلا گردیدهاست. بنابراین اگر بخواهی آن را به اصلش یعنی طلا برگردانی، برودت آن را به درون انتقال ده، حرارت آن آشکار میشود. سپس خشکی آن را به درون منتقل کن، در نتیجه، رطوبت آشکار و نقره تبدیل به طلا میشود.
دستاوردها
نوآوری انواع گوناگونی از وسایل آزمایشگاهی، از جمله عنبیق به اسم او ثبت شدهاست. کشف مواد شیمیایی متعددی همچون هیدرو کلریک اسید، نیتریک اسید، تیزاب (مخلوطی از دو اسید یاد شده که از جمله اندک موادی است که طلا را در خود حل میکند)، سیتریک اسید (جوهر لیمو) و استیک اسید (جوهر سرکه)، همچنین معرفی فرایندهای تبلور و تقطیر که هر دو سنگ بنای شیمی امروزی به شمار میآیند، از جمله یافتههای اوست. او همچنین یافتههای دیگری دربارهٔ روشهای استخراج و خالص سازی طلا، جلوگیری از زنگ زدن آهن، حکاکی روی طلا، رنگرزی و نم ناپذیر کردن پارچهها و تجزیهٔ مواد شیمیایی ارائه داد. از جمله اختراعهای دیگر او، قلم نوری است. قلمی که جوهر آن در تاریکی نیز نور میدهد. (احتمالاً با استفاده از خاصیت فسفرسانس این اختراع را انجام دادهاست.) در آخر، بذر دسته بندی امروزی عنصرها به فلز و نافلز را میتوان در دست نوشتههای وی یافت.
پانویس
- ↑ برگرفته از پشت جلد کتاب شیمی ۳ سال سوم دبیرستان
- ↑ Abu Musa Jabir ibn Hayyan (Arabian alchemist) - Britannica Online Encyclopedia
- ↑ ۳٫۰ ۳٫۱ "Abu Musa Jabir ibn Hayyan". Encyclopædia Britannica Online. http://www.britannica.com/eb/article-9043128/Abu-Musa-Jabir-ibn-Hayyan. Retrieved 11 February 2008.
- ↑ S.N. Nasr, "Life Sciences, Alchemy and Medicine", The Cambridge History of Iran, Cambridge, Volume 4, 1975, p. 412: "Jabir is entitled in the traditional sources as al-Azdi, al-Kufi, al-Tusi, al-Sufi. There is a debate as to whether he was an Arab from Kufa who lived in Khurasan or a Persian from Khorasan who later went to Kufa or whether he was, as some have suggested, of Syrian origin and later lived in Persia and Iraq".
- ↑
- William R. Newman, Gehennical Fire: The Lives of George Starkey, an American Alchemist in the Scientific Revolution, Harvard University Press, 1994. p.94: "According to traditional bio-bibliography of Muslims, Jabir ibn Hayyan was a Persian alchemist who lived at some time in the eight century and wrote a wealth of books on virtually every aspect of natural philosophy"
- William R. Newman, The Occult and Manifest Among the Alchemist, in F. J. Ragep, Sally P Ragep, Steven John Livesey, Tradition, Transmission, Transformation: Proceedings of Two Conferences on pre-Modern science held at University of Oklahoma, Brill, 1996/1997, p.178: "This language of extracting the hidden nature formed an important lemma for the extensive corpus associated with the Persian alchemist Jabir ibn Hayyan"
- Henry Corbin, "The Voyage and the Messenger: Iran and Philosophy", Translated by Joseph H. Rowe, North Atlantic Books, 1998. p.45: "The Nisba al-Azdin certainly does not necessarily indicate Arab origin. Geber seems to have been a client of the Azd tribe established in Kufa"
- Tamara M. Green, "The City of the Moon God: Religious Traditions of Harran (Religions in the Graeco-Roman World)", Brill, 1992. p.177: "His most famous student was the Persian *Jabir ibn Hayyan (b. circa 721 C.E.), under whose name the vast corpus of alchemical writing circulated in the medieval period in both the east and west, although many of the works attributed to Jabir have been demonstrated to be likely product of later Ismaili' tradition."
- David Gordon White, "The Alchemical Body: Siddha Traditions in Medieval India", University of Chicago Press, 1996. p.447
- William R. Newman, Promethean Ambitions: Alchemy and the Quest to Perfect Nature, University of Chicago Press, 2004. p.181: "The corpus ascribed to the eight-century Persian sage Jabir ibn Hayyan.."
- Wilbur Applebaum, The Scientific revolution and the foundation of modern science, Greenwood Press, 1995. p.44: "The chief source of Arabic alchemy was associated with the name, in its Latinized form, of Geber, an eighth-century Persian."
- Neil Kamil, Fortress of the Soul: Violence, Metaphysics, and Material Life in the Huguenots New World, 1517-1751 (Early America: History, Context, Culture), JHU Press, 2005. p.182: "The ninth-century Persian alchemist Jabir ibn Hayyan, also known as Geber, is accurately called pseudo-Geber since most of the works published under this name in the West were forgeries"
- Aleksandr Sergeevich Povarennykh, Crystal Chemical Classification of Minerals, Plenum Press, 1972, v.1, ISBN 0-306-30348-5, p.4: "The first to give separate consideration to minerals and other inorganic substances were the following: The Persian alchemist Jabir (721-815)..."
- George Sarton, Introduction to the History of Science, Pub. for the Carnegie Institution of Washington, by the Williams & Wilkins Company, 1931, vol.2 pt.1, page 1044: "Was Geber, as the name would imply, the Persian alchemist Jabir ibn Haiyan?"
- Dan Merkur, in The psychoanalytic study of society (eds. Bryce Boyer, et al.), vol. 18, Routledge, ISBN 0-88163-161-2, page 352: "I would note that the Persian alchemist Jabir ibn Hayyan developed the theory that all metals consist of different 'balances' ..."
- Anthony Gross, The Dissolution of the Lancastrian Kingship: Sir John Fortescue and the Crisis of Monarchy in Fifteenth-century England, Paul Watkins, 1996, ISBN 1-871615-90-9, p.19: "Ever since the Seventy Books attributed to the Persian alchemist Jabir Ibn Hayyan had been translated into Latin ...."
- A Dictionary of the History of Science by by Anton Sebastian - p. 241
- The Structure and Properties of Matter by Herman Thompson Briscoe - p. 10
- The Tincal Trail: A History of Borax by Edward John Cocks, Norman J. Travis - p. 4
- ↑ The Voyage and the Messenger: Iran and Philosophy By Henry Corbin Translated by Joseph H. Rowe Published by North Atlantic Books, 1998 ISBN 1-55643-269-0, 9781556432699
- ↑ برگرفته از پشت جلد کتاب شیمی ۳ سال سوم دبیرستان
- ↑ Islamic Medical Manuscripts
منابع
- دکتر زکی نجیب محمود - جابر بن حیّان - مجمع ذخایر اسلامی- چاپ خیّام - نوبت چاپ: دوم - آبان ۱۳۶۲.
- «جابربن حیّان» (فارسی). دانشنامهٔ جهان اسلام. بازبینیشده در ۹ اسفند ۱۳۸۷.
- دهخدا، علیاکبر. لغتنامه دهخدا جلد۱۶ شماره مسلسل۴۶. زیر نظر دکتر محمد معین. تهران: دانشگاه تهران، سازمان لغتنامه، ۱۳۳۴. ۷.
- شیمی و آزمایشگاه- برهم کنش مواد، نویسندگان: احمد روح الهی، سیف الله جلیلی، دوست محمد سمیعی و حسن حذر خانی، ناشر:شرکت چاپ و نشر کتابهای درسی ایران:تهران، سال چاپ: ۱۳۸۶
پیوند به بیرون
- جابر بن حیان در لغتنامهٔ دهخدا، سرواژهٔ «جابر».
[نهفتن] بزرگان جهان اسلام در سدههای یکم تا هشتم هجری - ابن اثیر
- ابو کمیل
- ابونواس
- بتانی
- وقیدی
- ابوالوفای بوزجانی
- معری
- بغدادی
- بیرونی
- تقیالدین
- الحازن
- کاشانی
- ابراهیم ادهم
- کندی
- ابن رشد
- ابنسینا
- ادریسی
- ابوسعید گرگانی
- فرغانی
- ابوالفرج
- ابوالفدا
- عباس ابن فرناس
- مسعودی
- مروزی
- مقریظی
- ابن مقفع
- فخر رازی آملی
- ابن ندیم
- ابن خلدون
- ابراهیم ابن صنعان
- جابر ابن حیان
- حسن الوزن
- خاقانی
- خیام نیشابوری
- خجندی
- خوارزمی
- ابن البنا
- ابن فضلان
- ابن نفیس
- محمد فرزند عبدالله
- شیخ یوسف سروستانی
- ابوسعید ابوالخیر
- علی قوشچی
- صوفی
- عطار نیشابوری
- ابن بطوطه
- ابن رومی
- مویدفیالدین شیرازی
- حاجی بکتاش والی
- حلاج
- زکریا رازی
- قاضیزاده رومی
- نصیرالدین طوسی
- اقلیدسی
- سعدی
- سنان
- جریر طبری آملی
- فارابی
- بیضاوی
- غزالی
- نظامی
- ابن حزم
- ابن عربی
- مولوی
امتیاز : نتیجه : امتیاز توسط نفر مجموع امتیاز :
برچسب ها :
بازدید : 2948 نويسنده: [cb:post_author_name] | [cb:post_create_date] ساعت [cb:post_create_time]
عمود و عمود منصف
ç عمود منصف ( perpendiculaar bisector):
عمود به معنی ستون، چوب خیمه و گرز می باشد و در ریاضی خطی که بر یک پاره خط عمود شود و آن را نصف کند را عمود منصف آن پاره خط گویند. خط d عمود منصف پاره خط AB است.

ç فاصله نقطه از خط:
فاصله نقطه از خط کوتاهترین پاره خط بین نقطه و آن خط می باشد. هر گاه از نقطه ای خارج از یک خط بر آن عمودی رسم کنیم، فاصله آن نقطه از پای عمود ، فاصله نقطه از خط نامیده می شود.
PH فاصله نقطه P از خط d می باشد.این فاصله کوتاهترین مسیر از نقطه p به خط d می باشد.


ç ترسیم های هندسی:
یکی از بخش های هندسه رسم کردن خطوط و اشکال هندسی می باشد. این بخش از هندسه کاربرد زیادی در نقشه کشی ساختمان طراحی صنعتی، معماری، رسم فنی و ... دارد. خط کشی، پرگار، گونیا و نقاله مهمترین ابزار برای کشیدن یک شکل دقیق و منظم می باشند. رسم خط عمود بر یک خط ، رسم عمود منصف یک پاره خط ، رسم نیمساز یک زاویه و ... نمونه هایی از ترسیم های هندسی هستند.

رسم کردن خط عمود بر یک خط
با استفاده از گونیا می توان از نقطه ای روی یک خط یا خارج آن خطی به آن خط عمود کرد ، در شکلهای زیر روش این کار را مشاهده می کنید.

رسم کردن عمود منصف یک پاره خط

رسم کردن نیمساز یک زاویه

مراحل رسم:
1. از رأس زاویه کمان دلخواهی می زنیم تا اضلاع زاویه را در دو نقطه قطع کند.
2. سوزن پرگار را روی این دو نقطه گذاشته و دو کمان می زنیم.
3. محل برخورد دو کمان را به رأس زاویه وصل می کنیم.
رسم کردن خط عمود بر یک خط با پرگار
الف) از نقطه خارج از یک خط:
سوزن پرگار را روی نقطه مفروض گذاشته، کمانی می زنیم و قسمتی از خط را به پاره خط تبدیل می کنیم سپس عمود منصف این پاره خط را رسم می کنیم.
ب) از نقطه روی یک خط:
سوزن پرگار را روی نقطه گذاشته و قسمتی از خط را به پاره خط تبدیل می کنیم و سپس عمود منصف آنرا رسم می کنیم.

رسم مثلث
حالت اول: رسم مثلث با در اختیار داشتن دو ضلع و زاویه بین آن ها.

حالت دوم: رسم مثلث با در اختیار داشتن دو زاویه و ضلع بین آن ها:

حالت سوم: رسم مثلث با در اختیار داشتن سه ضلع


1. هر نقطه روی عمود منصف یک پاره خط از دو سر آن پاره خط به یک فاصله است.
2. هر نقطه از دو سر پاره خط به یک فاصله باشد، روی عمود منصف آن پاره خط واقع است.
3. دو خط عمود بر یک خط موازیند.
4. شرط اینکه با سه پاره خط به طولی های c , b, a بتوان مثلث رسم کرد آن است که b+c>a , a+c>b , a+b>c باشد.
5. از هر نقطه روی یک خط و یا خارج از آن فقط یک خط می توان بر آن عمود رسم کرد.
6. از هر نقطه واقع در خارج یک خط فقط یک خط می توان با آن موازی رسم کرد.
سوال: با استفاده از پرگار و خط کش غیر مدرج یک زاویه قائمه را به سه قسمت مساوی تقسیم کنید.

حل: به اندازه دلخواه روی نیم خط ox پاره خط OA را جدا می کنیم و به اندازه OA و به مرکز O مثلث OAB را رسم می کنیم. چون مثلث
 متساوی الاضلاع است ، پس زاویه آن ˚60 است ، نیمساز زاویه ˚60 را رسم می کنیم ، بدین ترتیب زاویه قائمه به سه زاویه مساوی تقسیم می شود.
متساوی الاضلاع است ، پس زاویه آن ˚60 است ، نیمساز زاویه ˚60 را رسم می کنیم ، بدین ترتیب زاویه قائمه به سه زاویه مساوی تقسیم می شود.

خط و نقطه

نقطه
نقطه جایی را در فضا نشان می دهد.
نقطه طول، عرض و ضخامت ندارد . از حرکت نقطه، خط بوجود می آید.
خط
از دو طرف نامحدود است یا امتداد دارد.
برای نامگذاری خطها و نقاط معمولا خطها را با حروف کوچک و نقاط را با حروف بزرگ الفبای لاتین نمایش می دهند.
نیم خط
از یک طرف محدود (بسته) و از طرف دیگر نامحدود است یا امتداد دارد.
برای نامگذاری از یک حرف بزرگ و یک حرف کوچک لاتین استفاده می شود. مانند نیم خط Ax.

پاره خط
از هر دو طرف محدود یا بسته است.
برای نامگذاری آن از دو حرف بزرگ لاتین استفاده می شود. مانند پاره خط AB.

 انطباق (superposition)
انطباق (superposition)انطباق به معنی منطبق شدن، برابر شدن با، یکسان گشتن با، می باشد. در هندسه، بر روی هم نهادن دو شکل (دو مثلث یا دو زاویه ) معمولی ترین روش برای بررسی تساوی آن هاست. دو شکل که بر هم منطبق می شوند، با هم مساویند و دو شکل که با هم مساوی باشند، می توانند بر هم منطبق شوند.

1. اگر n نقطه واقع بر یک خط راست در نظر گرفته شوند ، تعداد نیم خطهای روی این خط 2n و تعداد پاره خطهای روی این خط
 می باشد.
می باشد.مثال: اگر روی یک خط 10 نقطه مشخص شده باشد، تعداد نیم خطها و پاره خطهای ایجاد شده را حساب کنید.

2. در شکل زیر m وسط پاره خط AB و O نقطه ای در سمت چپ A است.
در این صورت

3. در شکل زیر M وسط پاره خط AB و O نقطه ای بین A و M است. در این صورت :

 زاویه (angle)
زاویه (angle)زاویه به معنی گوشه است و در اصطلاح هندسه « مجموعه نقاط یک صفحه که محدود به دو نیم خط با مبدا مشترک می باشند » منظور از راویه فقط دو نیم خط هم مبدا نمی باشد، بلکه آن مقداری است که دو نیم خط از هم باز می شوند.
زاویه های متقابل به رأس (vertical angles):
دو زاویه که رأس مشترک داشته باشند و ضلع های آن ها دو به دو بر امتداد یکدیگر و در جهات مختلف باشند « متقابل به راس » می گوییم.

دو زاویه مجاور:
دو زاویه را مجاور گویند هر گاه در رأس و یک ضلع مشترک باشند. مانند دو زاویه xÔy و yÔz در شکل مقابل:

زاویه های متمم (complementary angles):
دو زاویه را در صورتی متمم یکدیگر می گوییم که مجموع اندازه های آن ها ˚90 باشند، مانند زاویه های Ô۱ و Ô۲ در شکل مقابل:

زاویه های مکمل (supplementray angles):
دو زاویه را در صورتی مکمل یکدیگر می گوییم که مجموع اندازه های آن ها برابر ˚180 باشد، مانند زاویه های Ô۱ و Ô۲ در شکل مقابل:

زاویه های مجانب (asymptote angles):
دو زاویه را مجانب گویند هر گاه هم مجاور باشند و هم مکمل. مانند زاویه های
 در شکل مقابل:
در شکل مقابل:
اندازه زاویه و واحد آن:
اگر یک زاویه قائمه (راست) را به 90 قسمت مساوی تقسیم کنیم، هر قسمت
 زاویه قائمه است. این زاویه را زاویه یک درجه می نامیم و آن را به عنوان واحد اندازه گیری زاویه به کار می بریم.
زاویه قائمه است. این زاویه را زاویه یک درجه می نامیم و آن را به عنوان واحد اندازه گیری زاویه به کار می بریم.برای اندازه گیری زاویه از نقاله استفاده می کنیم.

 دایره (circle)
دایره (circle)دایره به معنی دور زننده و گردنده می باشد و در اصطلاح هندسه منحنی بسته ای است است در یک صفحه ، که همه نقاط آن از یک نقطه ثابت به نام مرکز دایره به یک فاصله اند.
شعاع دایره: پاره خطی است که یک سر آن مرکز دایره و سر دیگر آن روی محیط دایره می باشد.
کمان دایره: قسمتی از دایره که به دو نقطه روی محیط دایره محدود باشد.
وتر دایره: پاره خطی است که دو سر آن دو نقطه از دایره است.
قطر دایره: وتری است که از مرکز دایره می گذرد.


1. اگر دو زاویه مجاور باشند ، زاویه ای که بین نمیسازهای این دو زاویه تشکیل می شود ، نصف کل زاویه است.

2. نیمسازهای دو زاویه مجانب بر هم عمودند.

3. دو زاویه متقابل به رأس با هم مساویند.


4. نیم سازهای دو زاویه متقابل به رأس در یک امتدادند.

5. هر نقطه واقع بر نیمساز زاویه از دو ضلع زاویه به یک فاصله است و بالعکس هر نقطه که از دو ضلع یک زاویه به یک فاصله باشد ، بر نیمساز زاویه واقع است.

1. با توجه به شکل مقابل پاره خط AB به 3 قسمت مساوی تقسیم شده است. کدام رابطه صحیح می باشد؟

د)

ج)

ب) AB=۲AC
الف) AD>CB
2. با توجه به شکل زیر به جای نقطه چین در تساوی AD -(BC+ ...) = AB چه می توان نوشت؟

د) DE
ج) BD
ب) CD
الف) CE
3. نقطه C وسط پاره خط AE قرار دارد. اگر نقطه های B و D روی همان پاره خط طوری قرار گرفته باشند که AB=BC و CD=DE ، مقدار AD چند در صد مقدار AE است؟
د) 60 درصد
ج) 25 درصد
ب) 50 درصد
الف) 75 درصد
4. فاصله نقطه m از خط d برابر 5/2 سانتی متر است. چند نقطه روی خط d وجود دارد که تا m به فاصله 4 سانتی متر باشد؟

د ) هیچ نقطه
ج) 2 نقطه
ب) 3 نقطه
الف) 1 نقطه
5. متمم زاویه A چهار برابر زاویه A است؟ مکمل زاویه A چند درجه است؟
د) ˚158
ج) ˚152
ب) ˚168
الف) ˚162
6. مجموع سه زاویه ˚250 است، اگر اولی و دومی متقابل به رأس و دومی و سومی مکمل هم باشند، اندازه زاویه بزرگتر چند درجه است؟
د) ˚120
ج) ˚110
ب) ˚60
الف) ˚70
7. در شکل زیر دو زاویه Ô۱ و
امتیاز : نتیجه : امتیاز توسط نفر مجموع امتیاز :
برچسب ها : عمود منصف , فاصله نقطه از خط: , ترسیم های هندسی , رسم کردن خط عمود بر یک خط , رسم کردن نیمساز یک زاویه ,
بازدید : 2747
- بالا بودن الکترونگاتیوی اتمهای متصل به هیدروژن: برهمین اساس است که فلوئور (الکترونگاتیوترین عنصر) ، قویترین پیوند هیدروژنی و اکسیژن (الکترونگاتیوتر از نیتروژن) ، پیوند هیدروژنی قویتری درمقایسه با نیتروژن تشکیل میدهد. همچنین بار مثبت زیاد بر روی اتم هیدروژن ، زوج الکترون مولکول دیگر را بشدت جذب میکند و کوچک بودن اندازه اتم هیدروژن سبب میشود که ملکول دوم بتواند به آن نزدیک شود.




















